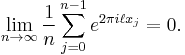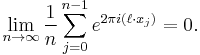Weyl's criterion
In mathematics, in the theory of diophantine approximation, Weyl's criterion states that a sequence  of real numbers is equidistributed mod 1 if and only if for all non-zero integers
of real numbers is equidistributed mod 1 if and only if for all non-zero integers 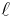 we have:
we have:
Therefore distribution questions can be reduced to bounds on exponential sums, a fundamental and general method.
This extends naturally to higher dimensions. A sequence
is equidistributed mod 1 if and only if 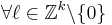 we have:
we have:
The criterion is named after, and was first formulated by, Hermann Weyl[1] .
See also
A quantitative form of the Weyl criterion is given by the Erdős–Turán inequality.
References
- ^ Weyl, H. (1916). "Ueber die Gleichverteilung von Zahlen mod. Eins,". Math. Ann. 77 (3): 313–352. doi:10.1007/BF01475864.